数据结构在学校的时候学的不认真，从头开始补吧。。。。
这次记一记表达式计算算法，主要利用堆栈实现，方便起见直接用的stl

算法流程

stack1.png

　　首先要将表达式转换为后缀表达式后缀表达式即 不包含括号，运算符放在两个运算对象的后面，所有的计算按运算符出现的顺序，严格从左向右进行（不再考虑运算符的优先规则，如：(2 + 1) * 3 ， 即2 1 + 3 *。转换成后缀表达式的原因是方便及更有条理的计算。

　　后缀表达式的转换过程如下图:
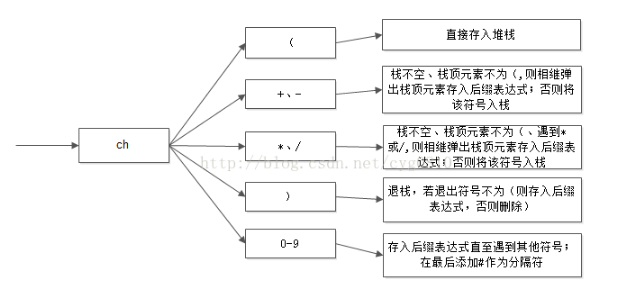
　　　　stack2.png

在转换过程中要注意以下几点：

  1. 在读到末尾’\0’后要注意把运算符堆栈内的剩余元素依次存入后缀表达式。
  2. 在读到一个数字后要将后面剩余的数字也依次存入后缀表达式，并且要最后添加#作为各个数字的分隔符。
  3. 在计算后缀表达式时将读入的数字字符串转换成整数并存入数字堆栈。
  4. 计算后缀表达式时遇到计算符号则从数字堆栈中退出2个数字，计算出值后再存入数字堆栈。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
#include <bits/stdc++.h>

using namespace std;
bool tran(char* exp, char* cal);    //转化为后缀表达式
int calculate(char* exp, char* cal);    /**表达式计算**/

int main()
{
    char exp[101], cal[101];
    while(gets(exp))
        cout << calculate(exp, cal) << endl;
    return 0;
}

int calculate(char* exp, char* cal)
{
    tran(exp, cal); //转化为后缀表达式
    cout << cal << endl;

    stack<int> numStack;
    int i = 0;

    while(cal[i] != '\0')
    {
        int res = 0;
        while(cal[i] >= '0' && cal[i] <= '9')   //将表达式中的字符串变为整数
        {
            res = res*10 + (cal[i]-'0');
            i++;
        }

        if(cal[i] == ' ')
        {
            i++;
            numStack.push(res);
        }
        else
        {
            int num1 = numStack.top();
            numStack.pop();
            int num2 = numStack.top();
            numStack.pop();

            switch(cal[i++])
            {
            case '+': numStack.push(num1 + num2); break;
            case '-': numStack.push(num1 - num2); break;
            case '*': numStack.push(num1 * num2); break;
            case '/': numStack.push(num1 / num2); break;
            }
        }
    }
    return (!numStack.empty()) ? numStack.top() : 0;

}

bool tran(char* exp, char* cal)  //将表达式转换为后缀表达式
{
    stack<char> charStack;
    int i = 0;
    int j = 0;
    char ch = exp[0];


    if(!(exp[strlen(exp)-1] >= '0' && exp[strlen(exp)-1] <= '9') ||
        exp[strlen(exp)-1] != ')' ||
        exp[strlen(exp)-1] != ' '
       )
        return false;

    while(ch != '\0')
    {
        switch(ch)
        {
        case '(':
            charStack.push(ch);
            break;

        case '+':
        case '-':
            while(!charStack.empty() && charStack.top() != '(')
            {
                cal[j++] = charStack.top();
                charStack.pop();
            }
            charStack.push(ch);
            break;

        case '*':
        case '/':
            while(!charStack.empty() &&
                  charStack.top() != '(' &&
                  (charStack.top() == '*' || charStack.top() == '/')
                 )
            {
                cal[j++] = charStack.top();
                charStack.pop();
            }
            charStack.push(ch);
            break;

        case ')':
            while(charStack.top() != '(' && !charStack.empty())
            {
                cal[j++] = charStack.top();
                charStack.pop();
            }
            charStack.pop();
            break;

        default:
            if(ch >= '0' && ch <= '9')
            {
                while(ch >= '0' && ch <= '9')
                {
                    cal[j++] = ch;
                    ch = exp[++i];
                }
                i--;
                cal[j++] = ' '; //用#将数隔开，便于计算
            }
            break;
        }
        ch = exp[++i];
    }
    /**在读到末尾'\0'后要注意把运算符堆栈内的剩余元素依次存入后缀表达式。**/
    while(!charStack.empty())
    {
        cal[j++] = charStack.top();
        charStack.pop();
    }
    cal[j] = '\0';
    return true;
}